(UERJ/2017) Observe a matriz.
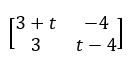
Anúncio
Para que o determinante dessa matriz seja nulo, o maior valor real de t deve ser igual a:
A) 1
B) 2
C) 3
D) 4
RESOLUÇÃO:
Para o determinante da matriz , basta realizar a operação de subtração entre o produto dos elementos que compõem a diagonal principal (a11 × a22) e o produto dos elementos da diagonal secundária (a12 × a21):
Então, tem-se:
(a11 × a22) − (a12 × a21) = 0
(3 + t) × (t − 4) − (−12) = 0
3t − 12 + t2 − 4t + 12 = 0
t2 − t = 0
t (t − 1) = 0
t = 0 ou t = 1
O maior valor real de t é 1.
Resp.: A
VEJA TAMBÉM:
– Questão resolvida sobre matriz, da UEL 2015
Publicidade
Anúncio. Role para continuar lendo.












