(Famerp/2019) Uma pessoa parada sobre a linha do equador terrestre apresenta uma velocidade tangencial, devido à rotação da Terra, de módulo próximo a 1 700 km/h.
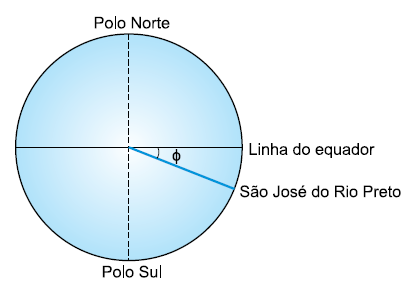
Sabendo que sen 21º = 0,36 e cos 21º = 0,93, uma pessoa em repouso sobre o solo, em São José do Rio Preto, cuja latitude é aproximadamente ϕ = 21º Sul, tem uma velocidade tangencial de módulo próximo a
A) 1 830 km/h.
B) 610 km/h.
C) 1 700 km/h.
D) 4 700 km/h.
E) 1 580 km/h.
RESOLUÇÃO:
A Terra gira com uma velocidade angular constante ($\omega$). Ou seja, ela demora o mesmo tempo para dar uma volta completa, não importa onde você esteja.No entanto, a velocidade tangencial ($v$) depende da distância até o eixo de rotação (o raio da trajetória circular).
v = ω. R , onde:
ω = velocidade angular
R = raio da circunferência que a pessoa descreve ao girar junto com a Terra
Pode-se dizer que ω. R = 1700
Quando a pessoa está no equador, o raio da trajetória é o próprio raio da Terra (R). O enunciado diz que a velocidade aqui é de 1700 Km/h.
Em São José do Rio Preto (ϕ = 21º Sul) , a pessoa não está girando no equador, mas em um círculo “menor” mais ao sul. A distância desse ponto até o eixo de rotação da Terra é menor.Olhando para a geometria (trigonometria), o raio de rotação nessa latitude (r) é a projeção do raio da Terra no plano horizontal daquela latitude:
r = R. cos ϕ
Voltando à equação (v = ω . r) , tem-se:
vSJRPreto = ω. (R. cos ϕ)
vSJRPreto = ω. R (cos ϕ) (lembre que ω. r = 1700 Km/h)
vSJRPreto =1700. 0,93
vSJRPreto = 1581 Km/h
Resp.: E
VEJA TAMBÉM:
– Questão resolvida sobre movimento circular, da Fema 2016
– Resolução da questão sobre movimento circular, da PUC GO 2023
Organize seus Estudos

Caderno Espiral Melissa Pautado 17x24 Colmeia
Preço: R$ 74,90














